Continúo este repaso, cuaderno de notas, apuntes, (o como lo queramos llamar) a la ciencia de datos usando Python. En esta ocasión me voy a centrar en los modelos predictivos, como la regresión lineal y polinómica (los modelos más habituales, pero no por ello poco interesantes), así como la regresión multivariante y los modelos multinivel.
Hace algun tiempo hice un curso pero que muy recomendable (pondré el enlace al final del post), del profesor Andrew Ng, que explicaba estos y otros conceptos mucho más avanzados, desde un punto de vista matemático y teórico… en este post no lo veremos así, sino sus aplicaciones prácticas y nos centraremos en su implementación en Python.
Todo lo que vamos a ver en este post se centra fundamentalmente en intentar definir una función tal que se ajuste a los valores que hayamos podido obtener de casos reales (las observaciones). Esa función nos permitiría “predecir”; nuevos valores que aún no hayamos visto.
Regresión Lineal
La regresión lineal (o Linear Regression en inglés), intentará calcular una linea recta que se ajuste todo lo posible a nuestro conjunto de observaciones.
¿Como se calcula? Internamente, la regresión lineal intenta establecer los parámetros que definen una función lineal ( y = mx + b ) tal que se minimice la suma de los errores cuadráticos de las observaciones a la linea definida por dicha función (se minimice la distancia de cada observación a la linea). En realidad es algo sencillo, pero aún así no tenemos que preocuparnos demasiado por ello ya que Python lo hará por nosotros.
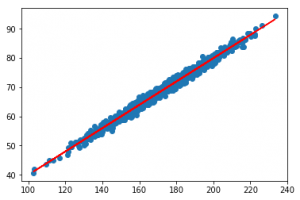
Veamos un ejemplo, generando algunos datos (completamente inventados y al azar, por supuesto) de cuanto pesa una persona en función de su altura:
%matplotlib inline
import numpy as np
from pylab import *
# Generamos datos "aleatorios"
altura = np.random.normal(170, 20, 1000)
peso = altura / 2.5 + np.random.normal(0, 1, 1000)
# scatter(altura,peso) ## Si quisieramos mostrar los datos sin la función de ajuste
# Con esta función tan sencilla calculamos la regresión lineal
from scipy import stats
slope, intercept, r_value, p_value, std_err = stats.linregress(altura, peso)
# Ahora lo representamos pintando también la regresión lineal
# como una linea roja sobre las observaciones (en azul)
import matplotlib.pyplot as plt
def predict(x):
return slope * x + intercept
fitLine = predict(altura)
plt.scatter(altura, peso)
plt.plot(altura, fitLine, c='r')
plt.show()
Hay más formas de calcular este ajuste: por ejemplo, si en lugar de trabajar con dos dimensiones, lo hiciésemos con datos tridimensionales, se aplica a menudo el método del Gradiente Descendiente, que itera para encontrar la linea que mejor se ajusta el contorno definido por los datos en una superficie, con un impacto computacional mayor. Este método se usa a menudo en datos con muchas dimensiones.
Medir el error
Algo que nunca debemos olvidar es que los modelos con los que vamos a trabajar cuando nos enfrentamos a problemas de esta naturaleza (data science, machine learning…) rara vez serán exactos, y lo que suelen ofrecer son resultados probables, estimaciones, etc. razón por la cual siempre debemos disponer de algún mecanismo que nos permita medir el error que producen nuestros cálculos, tanto para saber como de buenos son nuestros resultados, como para compararlos de una forma objetiva y cuantificable con la aplicación de otros métodos alternativos que puedan funcionar de forma distinta dependiendo de las propiedades de nuestro conjunto de datos.
Coeficiente de determinación (R-Cuadrado o R^2)
Esta forma de medición es: la fracción de la variación total de Y que se genera en nuestro modelo. Esta medición es aplicable en problemas de regresión lineal sencilla.
Error = 1 - ( suma de errores al cuadrado) / (suma de la variación al cuadrado de la media)
El error podrá ser un valor de 0 a 1, 0 significa que hay un error máximo, y 1 es que se capturó totalmente la varianza de los datos en el ajuste lineal, el resultado perfecto.
En el ejemplo anterior, su cálculo es tan sencillo como leer el valor del parámetro devuelvo por la función durante el calculo de la regresión lineal, de nombre r_value.
# Lo elevamos al cuadrado para obtener R^2
r_value ** 2
# OUT: 0.98554872784874969
Como podemos ver, el valor es muy cercano a uno, lo que significa que nuestra función se ajusta casi perfectamente a las observaciones. Es una buena aproximación.
Regresión polinómica
En muchas ocasiones nuestros datos no se ajustan a una linea recta, sino que describen curvas más o menos complejas. En estos casos en los que las relaciones no son lineales podemos realizar un ajuste a una función polinómica del orden que consideremos que se ajustará mejor a la complejidad de las curvas descritas por nuestros datos.
- Polinomio de segundo orden: y = ax^2+bx+c
- Polinomio de tercer oden: y = ax^3 + bx^2 + cx + d
Polinomios de mayor nivel producen curvas más complejas… aunque hay que intentar no sobrepasarse, ya que se puede producir un overfitting, es decir, nos ajustamos tanto a los datos de nuestras muestras que aparentemente se produce un ajuste perfecto, pero si nuestras muestras tienen muchas varianzas, probablemente no sirva como modelo predictivo, y tenga grandes errores cuando aparezcan nuevas muestras.
Lo ideal es intentar visualizar o al menos comprender los datos con los que contamos primero, para imaginar como de compleja será realmente la curva que subyace aparentemente bajo estos datos. Si conseguimos visualizar esta curva, podemos comprender si se está ajustando a los outliers, o si está realizando una correcta generalización de los datos de muestra. Tener un error bajo en el ajuste polinómico significa únicamente que nos estamos ajustando a los datos de muestra… no que vayamos a realizar predicciones correctas.
%matplotlib inline
from pylab import *
import numpy as np
# creamos algunas muestras aleatorias, en las que el numero de ventas de productos
# se reduzca a medida que aumenta su precio
np.random.seed(2)
itemPrices = np.random.normal(3.0, 1.0, 1000)
purchaseAmount = np.random.normal(50.0, 10.0, 1000) / itemPrices
# calculamos la curva polinomica de 4 grado que se ajusta a los datos
# usando la funcion polyfit
x = np.array(itemPrices)
y = np.array(purchaseAmount)
p4 = np.poly1d(np.polyfit(x, y, 4))
# pintamos la muestra y la funcion polinomica en rojo para ver como se ajusta
import matplotlib.pyplot as plt
xp = np.linspace(0, 7, 100)
plt.scatter(x, y)
plt.plot(xp, p4(xp), c='r')
plt.show()
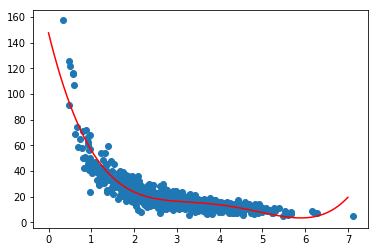
El resultado, como vemos a continuación, es una función que parece ajustarse bastante correctamente a nuestros datos de muestra. No parece haber un overfitting, ya que en los espacios entre las muestras y los outliers (el primer y el ultimo punto, por ejemplo) la curva no describe “subidas y bajadas”; sin sentido.
Medir el error
Con lo que sabemos hasta ahora, podemos medir el error utilizando el R^2 SCORE.
from sklearn.metrics import r2_score
r2 = r2_score(y, p4(x))
print(r2)
# OUT: 0.82937663963
Como sabemos, si se acerca a 0 el ajuste es pésimo, y cuanto más cerca de 1 esté, mejor se ajusta a nuestros datos de meustra. En este caso el valor indica que es un ajuste bastante correcto.
Regresión multivariante
En los ejemplos que hemos visto hasta ahora, hemos realizado ajustes a datos que variaban en función de una única variable. Sin embargo en muchos casos lo que intentamos predecir varia en función de muchas variables que tienen influencia en ello. Por ejemplo, en el caso de la venta de viviendas, el precio puede variar en función de los años que lleva construida, los metros cuadrados, el numero de baños, número de chimeneas, de plantas… en este caso tendremos que usar un tipo de regresión que se ajusta en función de un gran numero de variables, y que se llama regresión multivariante o_ regresión múltiple_. Por ejemplo:
precio = a + b1* años + b2 * metros + b3 * baños
Los coeficientes b1, b2 y b3 nos permiten determinar como de importante es cada factor, sin embargo, para que la formula tenga sentido, cada uno de los 3 factores años, metros y baños deben estar normalizados, es decir, estar en escalas similares. Si esto se cumple y están normalizados, podremos seguir utilizando el R^2 como medida de ajuste a los datos de muestra.
Es importante tener en cuenta que este tipo de regresión no puede emplearse con variables o características que sean dependientes de otras que formen parte de la fórmula. Por ejemplo, en este caso, parece lógico que el número de baños dependa de la superficie en metros de la casa, en tal caso la formula no tendrá en cuenta esta dependencia por lo que podría arrojar predicciones erróneas… es importante detectar estas dependencias y eliminar todas las características dependientes que no sean realmente relevantes.
Ejemplo
Para ilustrar esto, voy a utilizar un ejemplo del curso que recomiendo realizar si os interesa profundizar en este tema, os dejo el enlace aquí: https://www.udemy.com/data-science-and-machine-learning-with-python-hands-on/
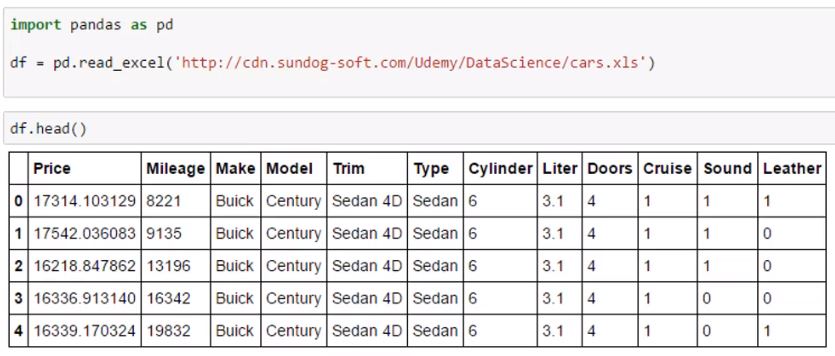
Partimos de un documento Excel que contiene un catálogo de vehículos con algunas de sus características:
Lo que vamos a hacer es utilizar algunas de sus características ordinales (numero de cilindros, puertas, etc) para obtener un modelo predictivo de su precio. Vamos a omitir las características categóricas, como el modelo, ya que no hay una forma rápida de convertir esto en factores que emplear en nuestras fórmulas (podria hacerse, asignando valores que tengan algun orden y significado a cada una de las categorías).
import statsmodels.api as sm
from sklearn.preprocessing import StandardScaler
scale = StandardScaler()
# determinamos que queremos calcular (variable y)
# y a partir de que caracteristicas (variable X)
X = df[['Mileage', 'Cylinder', 'Doors']]
y = df['Price']
# Aplicamos la funcion que nos normaliza automaticamente todos los valores
# para que sean comparables y los coeficientes b1, b2 y b3 tengan sentido
X[['Mileage', 'Cylinder', 'Doors']] = scale.fit_transform(X[['Mileage', 'Cylinder', 'Doors']].as_matrix())
print (X)
# OUT: dataset de entrenamiento del modelo OLS
Mileage Cylinder Doors
0 -1.417485 0.527410 0.556279
1 -1.305902 0.527410 0.556279
2 -0.810128 0.527410 0.556279
3 -0.426058 0.527410 0.556279
4 0.000008 0.527410 0.556279
5 0.293493 0.527410 0.556279
6 0.335001 0.527410 0.556279
# Usamos el modelo Ordinary Least Square del paquete statsmodel y creamos el modelo
# a partir de las caracteristicas de X y los valores del vector y
est = sm.OLS(y, X).fit()
est.summary()
Los resultados que arroja el modelo OLS serán los siguientes
y.groupby(df.Doors).mean()
# OUT: resultado
Doors
2 23807.135520
4 20580.670749
Modelos multinivel
He mencionado un par de veces que hay que evitar tener en cuenta, en este tipo de regresiones, las dependencias entre las caracteristicas que se consideran. Sin embargo en muchas ocasiones la variabilidad de los datos nace de estas interdependencias, que pueden ser muy complejas.
Imagina por ejemplo de qué depende tu salud: del estado de cada una de tus células, de tus organos, de tu actividad fisica, de tu trabajo, de tu familia (de su propia salud y de los niveles de estrés que te producen). Pero a su vez, cada uno de estos elementos depende de otras cuestiones, como la calidad del aire del lugar donde realizas la actividad física, y esto depende a su vez de cuestiones estatales como las politicas de polucion, energias renovables, etc.
Es solo un ejemplo, pero es evidente que existe una interdependencia jerárquica a varios niveles, para cada una de las características que determinan tu salud. Este tipo de análisis se realiza mediante la aplicación de modelos multinivel, sin embargo es un tema difícil y peliagudo, que merece su propio curso y que nunca he visto aplicado, así que no puedo escribir acerca de él.
Referencias y créditos
He redactado este artículo a partir de mi aprendizaje en las siguientes fuentes:
- Curso Data Science: https://www.udemy.com/data-science-and-machine-learning-with-python-hands-on