No soy ningún experto (de momento, mwahaha) pero siempre me han interesado la implementación de sistemas relacionados con la inteligencia artificial y el aprendizaje automático. Últimamente está en boga, por lo que he pensado en escribir algunos posts hasta donde mi conocimiento alcance, para aquellos que sin tener idea de estadística o machine learning quieran disponer de un cheatsheet para recordar o aprender conceptos muy relacionados con estos asuntos.
En el primero de los post abordaré muchos principios básicos de estadística que sin embargo son muy importantes para definir los procesos de aprendizaje automático, y que seguro que hemos olvidado desde nuestra época de estudiantes. Ya que Python es uno de los lenguajes más utilizados para la implementación de este tipo de cálculo, será el lenguaje en el que pondré los ejemplos de generación y análisis de datos.
Trataremos los siguientes temas:
- Media, mediana y moda
- Varianza y desviación estándar
- Función de densidad de probabilidad
- Percentiles y momentos
- Covarianza y correlación
- Probabilidad condicional
- Teorema de Bayes
¡Allá vamos!
Media, mediana y moda
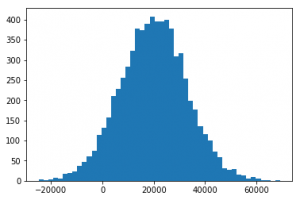
Generamos algunos datos de prueba, por ejemplo una distribución normal centrada en el valor 20000, con una desviación estándar de 13000 y 7000 valores.
# Generamos el conjunto de datos de prueba
import numpy as np
ingresos = np.random.normal(20000, 13000, 7000)
# Representamos los datos graficamente
%matplotlib inline
import matplotlib.pyplot as plot
plot.hist(ingresos, 50)
plot.show()
La figura siguiente representa un histograma con 50 columnas, a partir de los datos anteriores:
Media
Todos sabemos como calcular la media, se suman todos los valores de una colección y se dividen entre el número de valores que se sumaron. En Python es tan fácil como esto:
```python np.mean(ingresos) # OUT: 19935.065866607401
Como se ve en el comentario del snippet anterior, el resultado es cercano a 20000, lo cual tiene sentido ya que es como hemos generado nuestro conjunto aleatorio de datos de prueba.
La media es muy sensible a los conocidos _outliers_, estos son valores que se salen de la distribución normal, y que tienen un gran impacto en este cálculo, por lo que a menudo si existen unos pocos outliers pueden generar resultados muy engañosos. En el ejemplo anterior, si existiese un ciudadano que tuviese de ingresos 8.000.000€ (muy alejado de 19935 que es lo normal en nuestra distribución) la media se resiente bastante, de hecho en nuestro ejemplo pasaría a ser: 21074, con un solo outlier.
### Mediana
La mediana se calcula ordenando los valores de menor a mayor, y cogiendo aquel situado en el centro de la colección. Si el numero de elementos es par, se calcula la media de los dos valores centrales. Este tipo de cálculo es menos sensible a los outliers, ya que estos estarán situados en los extremos de la colección, pero no afectan proporcionalmente a su valor.
```python np.median(ingresos) # OUT: 19978.045647046532
Si realizamos el mismo cálculo incluyendo el outlier anterior, la mediana apenas varía:
ingresos = np.append(ingresos, [8000000])
np.median(ingresos) # OUT: 19978.345264457148
Moda
La moda permite obtener cual es el valor más común dentro de una colección. Presenta la ventaja de que los outliers son prácticamente descartados de forma natural, y que además pueden emplearse sobre tipos de datos que no sean continuos (por ejemplo categorías de productos).
Hay que tener en cuenta que puede utilizarse sobre valores discretos sin problema, pero que es difícil que encaje en un caso en el que deba emplearse sobre valores continuos (por no decir nunca).
Por esta razón, para probarlo, vamos a generar un conjunto de datos con valores discretos, como pueden ser cuerdas en instrumentos de cuerda (inventado por supuesto).
cuerdas = np.random.randint(low=1, high=12, size=100) cuerdas
# OUT: array([10, 5, 2, 5, 4, 6, 6, 9, 3, 10, 11, 6, 11, 4, 9, 5, 8, 11, 7, 3, 3,
9, 2, 2, 10, 7, 10, 1, 7, 8, 3, 5, 7, 11, 5, 6, 9, 11, 9, 7, 8, 11, 6, 1, 2, 4, 6,
7, 10, 10, 9, 3, 9, 10, 1, 6, 9, 6, 5, 8, 10, 9, 9, 7, 1, 5, 3, 11, 1, 7, 5, 3, 8,
10, 3, 5, 11, 7, 11, 11, 9, 11, 6, 3, 5, 1, 5, 4, 2, 5, 11, 11, 1, 8, 11, 1, 6, 1,
8, 3])
Y a continuación calculamos la moda empleando la libreria scipy.
from scipy import stats
stats.mode(cuerdas)
# OUT: ModeResult(mode=array([11]), count=array([14]))
Podemos ver que según nuestro conjunto de datos, el numero de cuerdas más habitual es 11, que existe 14 veces en nuestros datos de muestra.
Resumiendo
A modo de resumen, una imagen vale más que mil palabras.

From Wikipedia.org
Varianza y desviación estándar
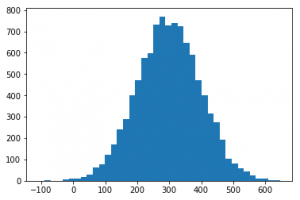
Pese a que a todos nos encantaría, no siempre los datos tienen esa forma “de campana”; que tanto facilitan las cosas, sino que la distribución de los valores pueden tener cualquier forma y esta es precisamente la que intenta calificarse mediante otras medidas de las que hablaré a continuación. Generamos un conjunto de datos para jugar, 10000 valores alrededor de 300, con una desviación estándar de 100.
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
ingresos = np.random.normal(300, 100.0, 10000)
plt.hist(ingresos, 40)
plt.show()
Varianza σ^2
La varianza es una de estas medidas de dispersión que se define como la media de las diferencias al cuadrado de los valores con respecto a la media, o lo que es lo mismo, es una forma de calcular la media del “desajuste”; de cada uno de los valores con respecto a la media del conjunto.
ingresos.var()
# OUT: 9844.0347762824531
Desviación estándar σ
En estadística se utiliza más habitualmente la desviación estándar que la varianza, y están intimamente relacionadas, de hecho, la Desviación estándar es la raíz cuadrada de la varianza. En Python es muy fácil calcular la desviación estándar, y como puede verse es cercano a 100 (lo cual tiene mucho sentido porque es el valor que indicamos al generar nuestro conjunto aleatorio).
ingresos.std()
# OUT: 99.217109292109768
La desviación estándar se utiliza para identificar los outliers en un conjunto de datos, simplemente observando cuantas “desviaciones estandar”; está un valor del conjunto alejado de la media. Cualquier valor que esté más de una desviación estándar alejado de la media puede considerarse fuera de lo normal.
Así en nuestro ejemplo, siendo la media cercana a 298, y la deviación estándar es 99, los valores por debajo de 199 y por encima de 397 serían considerados extraordinarios.
Población vs varianza muestral (population vs sample variance)
Debido a las propiedades de este tipo de calculo, es necesario distinguir si estamos trabajando con un conjunto de muestra (subconjunto de nuestros datos) o con todos los datos (población).
En los casos en los que es necesario trabajar con una muestra en lugar de con toda la población, se emplea una formula alternativa de la varianza, que consiste en que se dividen las varianzas al cuadrado por N-1, en lugar de N (siendo N el numero de muestras).
Función de densidad de probabilidad
Vamos a aclarar ahora qué es la función de densidad de probabilidad. Tal y como puede verse en el gráfico siguiente, que corresponde a una distribución normal, es posible establecer cual es la probabilidad de que un valor “caiga”; en cada una de las áreas determinadas de la función, o lo que es lo mismo, es la probabilidad de que ocurra un determinado valor.

From Wikipedia.org
En el diagrama se puede apreciar algo que se realiza habitualmente, por ejemplo, que consiste en calcular la probabilidad de ocurrencias fuera y dentro de las áreas determinadas por la desviación estándar.
En general, se suele hablar de probabilidad de una de estas ocurrencias de un valor específico dentro de ciertos rangos, ya que cuando no se trabaja con valores discretos, la probabilidad (calculada) de que ocurra un determinado valor es infinitamente pequeña (ya que entre el 0.1 y el 0.01 hay infinitos valores, por ejemplo, así que en ese caso no sería posible evaluar como de probable es que ocurra el valor 0.001.
Función de masa de probabilidad
Cuando trabajamos con valores discretos en lugar de continuos, esta problemática desaparece, y es posible entonces hablar de la probabilidad de que ocurra un valor específico, sin estimarlo dentro de un área. En este caso emplearemos la función de masa de probabilidad (o probability mass function).
Distribuciones en Python
Vamos a ver algunos ejemplos de distribuciones usando Python para generarlas y analizar sus propiedades.
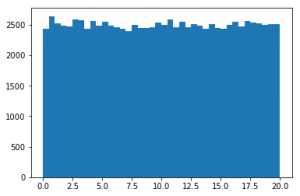
Distribución uniforme
En una distribución uniforme todos los valores tienen la misma probabilidad de ocurrir. En el siguiente ejemplo se genera una colección aleatoria de valores con distribución uniforme entre los valores 0 y 20.
# Distribución uniforme
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
values = np.random.uniform(0, 20.0, 100000)
plt.hist(values, 40)
plt.show()
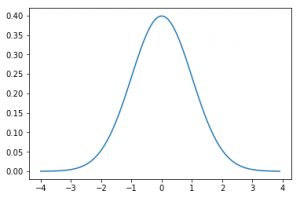
Distribución Gaussiana o Distribución normal
Es una de las estudiadas más habitualmente ya que de hecho aparece muy frecuentemente en casos reales. Se denomina gráfica de campana por la forma de su función de densidad, y suele ser simétrica respecto a algún parámetro.
# Distribución gaussiana
from scipy.stats import norm
import matplotlib.pyplot as plt
x = np.arange(-4,4,0.1)
plt.plot(x, norm.pdf(x))
# O si queremos generar valores con una determinada media (mu) y desviacion (sigma)...
import numpy as np
import matplotlib.pyplot as plt
mu = 5.0
sigma = 2.0
values = np.random.normal(mu, sigma, 10000)
plt.hist(values, 50)
plt.show()
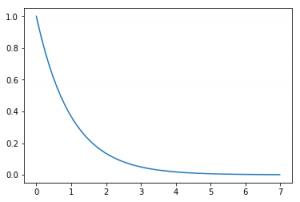
Función exponencial
Es otra función que se da muy a menudo, en la que los valores caen o aumentan muy rápido, conforme a una función exponencial.
# Función exponencial
from scipy.stats import expon
import matplotlib.pyplot as plt
x = np.arange(0, 7, 0.01)
plt.plot(x, expon.pdf(x))
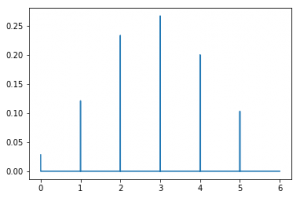
Función de masa de probabilidad
Se trata de las funciones de las que he hablado más arriba en este artículo. En Python pueden generarse empleando dos parámetros n y p, que permiten establecer la forma de la distribución.
# Función de masa de probabilidad
from scipy.stats import binom
import matplotlib.pyplot as plt
n, p = 10, 0.3
x = np.arange(0, 6, 0.001)
plt.plot(x, binom.pmf(x, n, p))
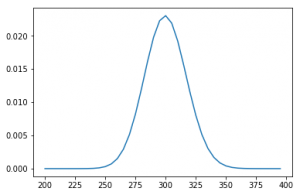
Distribución de Poisson
Se trata de una función que expresa a partir de la frecuencia media de que los sucesos ocurran, la probabilidd de que ocurra un determinado número de eventos durante cierto tiempo, en particular se utiliza para detectar la probabilidad de que ocurra un suceso raro o de probabilidad muy pequeña.
Por ejemplo en el caso a continuación, puede verse que la probabilidad de que, considerando que el eje X representa numero de personas que entran a una tienda en un mes, el hecho de que entren 325 personas es de aproximadamente del 0.7%.
# Función de masa de probabilidad de Poisson
from scipy.stats import poisson
import matplotlib.pyplot as plt
mu = 300
x = np.arange(200, 400, 5)
plt.plot(x, poisson.pmf(x, mu))
Percentiles y momentos
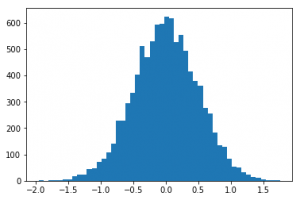
¿Sabes cuando has jugado demasiado a un videojuego y dice: has jugado 74 horas, estás en el 21%? Pues eso son los percentiles y se usan muchísimo. Vamos a ver un poco más.
La forma en que se describen es la siguiente: el percentil 99 representa el valor en el que, si ordenamos los valores, el 99% de las muestras son menores a dicho valor. En el ejemplo siguiente puede verse que el valor 0.00214… es el percentil 50, es decir, el 50% de los valores son menores a este valor.
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
vals = np.random.normal(0, 0.5, 10000)
plt.hist(vals, 50)
plt.show()
# Calculamos el percentil 50
np.percentile(vals, 50) # OUT: 0.0021422057356575478
# Calculamos el percentil 90
np.percentile(vals, 90) # OUT: 0.64070301059941248
Otro término relacionado que todos conocemos es el cuartil. El cuartil representa (en la función de distribución) los valores que contienen el 50% de los datos (25% de los datos a cada lado de la mediana). El área entre ambos cuartiles (a ambos lados de la media) es el área intercuartiles, que contiene por lo tanto el 50% de los valores.
Momentos
Los momentos son una forma de medir cuantitativamente la forma de una función de densidad de probabilidad. Matemáticamente pueden ser algo complejos de entender, pero aquí vamos a intentar verlo de forma sencilla, como me los explicaron a mi.
Los momentos son 4, cuya combinación permite conocer la forma de una distribución:
- La media
- La varianza
- La asimetría(skew): representa como de asimetricos son los datos sin necesidad de recurrir a su representación gráfica.
- Curtosis, apuntamiento o sesgo (kurtosis): representa como de afilado está la cima de la grafica, comparado con una distribución normal (a mayor curtosis, más afilado), es decir, el grado de concentración que presentan los valores de una variable alrededor de una zona central. La curtosis es positiva si esta por encima que la distribución normal, y negativa si está por debajo.

Asimetría: From Wikipedia.org

Curtosis: From Wikipedia.org
En Python, pueden calcularse sin necesidad de comprender sus fundamentos matemáticos, del siguiente modo:
# 1st Moment: Media
np.mean(vals)
# 2nd Moment: Varianza
np.var(vals)
# 3rd Moment: Asimetría
import scipy.stats as sp
sp.skew(vals)
# 4th Moment: Curtosis
sp.kurtosis(vals)
Covarianza y Correlación
La covarianza permite medir como dos variables varían conjuntamente respecto a sus medias. La covarianza por lo tanto es el dato más sencillo para determinar si existe una dependencia entre variables.
No voy a entrar en detalles de como se calculan, ya que utilizaremos Python para ello, y es más interesante centrarse en la interpretación del resultado.
Covarianza
Si la covarianza es cercana a 0, muy pequeña, significa que no hay mucha correlación entre ambas variables. Si la covarianza es grande (lejos de 0, pudiendo ser negativa si es una relación inversa), significa que hay correlación. Sin embargo, es dificil decidir qué es grande, ya que depende de las unidades que utilicemos para representar los datos.
La función numpy.cov es la que podremos usar para calcular la covarianza, sin embargo no vamos a ver ejemplos aquí ya que normalmente usaremos la correlación, porque es mas fácil de interpretar, como veremos a continuación.
Correlación
Es aquí donde la correlación entra en juego: consiste en dividir la covarianza por la desviación estandar de ambas variables, de forma que normalizamos el resultado. De este modo es más facil de interpretar:
- Si la correlación es de -1, hay una correlación inversa perfecta.
- Si la correlación es de 1, hay una correlación perfecta.
- Si la correlación es 0, no hay ninguna correlación entre ambas variables.
En Python…
# Generamos dos secuencias aleatorias (independientes, sin correlación)
%matplotlib inline
import numpy as np
from pylab import *
pageSpeeds = np.random.normal(3.0, 1.0, 1000)
visitAmount = np.random.normal(50.0, 10.0, 1000)
scatter(pageSpeeds, visitAmount)
# Calculamos los coeficientes de correlación
np.corrcoef(pageSpeeds, visitAmount)
# OUT:
# array([[ 1. , 0.08663524],
# [ 0.08663524, 1. ]])
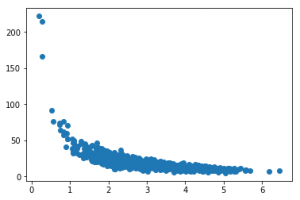
En el el caso anterior vemos como la función corrcoef de numpy nos devuelve el coeficiente de correlación de cada posible combinación de los arrays que establecemos como parámetros de la función. El resultado es 0.086… muy bajo, ya que no existe una relación entre ambas secuencias (como puede verse en la gráfica -scatter plot-)
# Hacemos que la cantidad de visitas tenga una relación con la velocidad de carga
visitAmount = np.random.normal(50.0, 10.0, 1000) / pageSpeeds
scatter(pageSpeeds, visitAmount)
# Calculamos el coeficiente de correlación
np.corrcoef(pageSpeeds, visitAmount)
# OUT:
array([[ 1. , -0.63098819],
[-0.63098819, 1. ]])
En este caso vemos como el coeficiente es mucho mayor (en terminos absolutos, ya que es negativo, lo que significa que hay una relación inversa). Si la correlación fuese perfecta (una proporción lineal, por ejemplo) el coeficiente sería 1 o -1.
Probabilidad condicional
Cuando construimos un motor de recomendación (ya que has comprado esto, quizás quieras comprar esto otro) a menudo necesitamos recurrir al concepto de probabilidad condicional.
La probabilidad condicional nos permite medir la probabilidad de que ocurra un evento considerando que ha ocurrido otro anteriormente. La notación puede ser un poco confusa pero la explico a continuación.
P(B|A) = P(A,B) / P(A)
Donde:
- P(A,B) es la probabilidad de que ocurran ambos acontecimientos, A y B, de forma independiente.
- P(B|A) es la probabilidad de que ocurra B si ha ocurrido A.
- P(A) es la probabilidad de que ocurra A.
Pongamos un ejemplo para verlo mas claro: supongamos que se hace un examen que consta de dos preguntas en una clase de bachillerato. El 60% de los estudiantes aprueba ambas preguntas -P(A,B)-. Sin embargo, la primera pregunta era más fácil, y la aprueban el 80% de los estudiantes -P(A)-. ¿Cuál es entonces la probabilidad de que los estudiantes que aprobaron la primera pregunta, aprueben también la segunda? -P(B|A)-.
La formula queda así:
P(B|A) = 0.6 / 0.8 = 0.75
O lo que es lo mismo, el 75% de los estudiantes que aprobaron la primera pregunta, habrán aprobado la segunda.
Ejemplo en Python
Vamos a intentar determinar que probabilidad hay de que una persona compre productos en una tienda en función de el rango de edad de dicha persona. Para ello, vamos a generar un par de vectores aleatoriamente, con una cantidad aleatoria de personas en edades de entre 20 y 60 años, y a asignar a cada bucket de edad una cantidad de compras, tambien aleatoriamente. Despues calcularemos la probabilidad.
from numpy import random
random.seed(0)
totals = {20:0, 30:0, 40:0, 50:0, 60:0}
purchases = {20:0, 30:0, 40:0, 50:0, 60:0}
totalPurchases = 0
for _ in range(100000):
ageDecade = random.choice([20, 30, 40, 50, 60])
purchaseProbability = float(ageDecade) / 150.0 # LO HACEMOS DEPENDIENTE DE LA EDAD
totals[ageDecade] += 1
rnd = random.random()
if (rnd < purchaseProbability):
totalPurchases += 1
purchases[ageDecade] += 1
# OUT totals: {20: 20001, 30: 19950, 40: 19911, 50: 20050, 60: 20088}
# OUT purchases: {20: 2721, 30: 4013, 40: 5297, 50: 6551, 60: 7990}
# OUT totalPurchases:26572
Ahora vamos a realizar los cálculos de probabilidad condicional para averiguar cual es la probabilidad de que alguien de 40 años compre algo. Nuestra notación será:
- V: de Veinte, es la probabilidad de tener 20 años.
- C: de Compra, es la probabilidad de comprar
Calculamos primero la probabilidad P(C|V), la probabilidad de que alguien de 20 años compre algo es simplemente el porcentaje de personas de 20 años que compraron algo, dividimos:
PCV = float(purchases[20]) / float(totals[20])
print('P(purchase | 20): ' + str(PCV))
# OUT: P(purchase | 20): 0.136043197840108
A continuación calculamos P(V), que es simplemente la probabilidad de tener 20 años en el total de personas de nuestro conjunto de datos (en el que recuerdo que había 100000 personas).
PV = float(totals[20]) / 100000.0
print("P(20): " + str(PV))
# OUT: P(20): 0.20001
P(C) es fácil de calcular también, es la probabilidad de que alguien compre algo independientemente de la edad, así que será el total de compras entre el total de personas.
PC = float(totalPurchases) / 100000.0
print("P(purchase):" + str(PC))
# OUT: P(purchase):0.26572
Ahora bien, si las compras y la edad fuesen independientes, entonces P(C|V) -0.13- sería muy parecido a P(C) -0.26-. No es así, por lo que vemos que C y V son dependientes (es evidente… en el conjunto que hemos creado lo hemos hecho dependiente a la fuerza).
Si quisiéramos saber cual es la probabilidad de que una persona tenga 20 años compre algo, de toda nuestra población, basta con calcular el producto de ambas probabilidades P(V)*P(C) = 0.053 = 5.3%.
Podemos calcular P(C,V), es decir, la probabilidad de tener 20 años y comprar algo, del total de la población (no solo de la gente que tiene 20). Sería así:
print("P(V, C)" + str(float(purchases[20]) / 100000.0))
# OUT: P(V, C) = 0.02721
Como podemos ver, P(C,V) y P(C)P(V) son iguales solo si las variables son independientes, en otro caso (como es este) serán distintas, ya que existe una relación de dependencia.
Finalmente podemos comprobar que nuestra función inicial funciona para calcular la probabilidad condicional de que una persona que tiene 20 años, compre algo:
P(C|V) = P(C,V) / P (V) = (purchases[20] / 100000) / PC = 0.13604
Resultado que coincide con nuestro cálculo basado en la intuición que hacíamos al principio del ejercicio, al calcular PCV. A veces no es necesario aplicar muchas matematicas y es posible obtener lo que buscamos de forma directa.
Teorema de Bayes
Lo último que vamos a ver en este artículo va a ser este famoso teorema que se emplea habitualmente en muchos problemas de estadística.
Este teorema se emplea a menudo para responder a preguntas en las que tenemos que A (causa) pueden ser una serie de circunstancias que nunca pueden ocurrir a la vez (por ejemplo, que una persona tome un medicamento o no) y B (efecto) es algo que puede ocurrir o no, con distinta probabilidad en función de A. ¿Cual es la probabilidad de que dado de que se observo un determinado efecto B, la causa haya sido A?
P(A|B) = P(A)P(B|A) / P(B)
Si observamos la función con detalle, veremos que en realidad es lo mismo que calcular la probabilidad de que suceda A y B (habiendo ocurrido A), es decir, el producto de ambas probabilidades en esa rama, dividido entre la probabilidad total de A.
P(A|B) = P(A & B) / P(B)
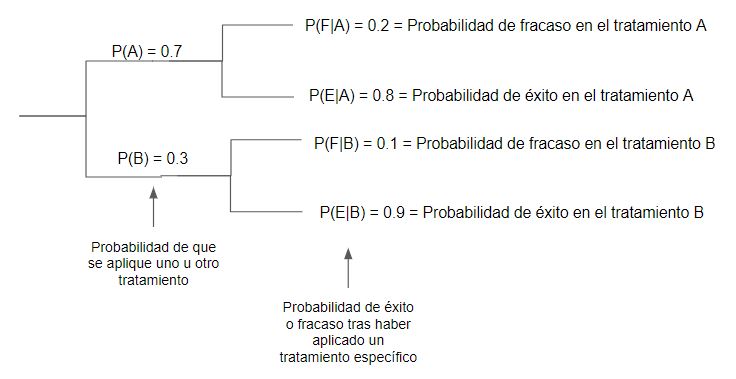
Veamoslo con un ejemplo. Tenemos dos medicamentos A y B, que se prueban en distintos pacientes. El porcentaje de fracaso con el medicamento A es del 20%, y el del B del 10%. Sin embargo, el medicamento B es mas caro, por lo que solo se aplica el 30% de las veces (en el 70% de pacientes restantes se emplea el A). Un paciente recibio tratamiento pero NO se curó. ¿Cual es entonces la probabilidad de que se le haya tratado con el medicamento A?
O lo que es lo mismo: P(A|F) = probabilidad de que haya tomado el medicamento A habiendo fracasado el tratamiento.
P(A|F) = (0.7 \* 0.2) / ( (0.7\*0.2) + (0.3*0.1) ) = 0.823
Es decir, en este caso, si se ha observado un paciente cuyo tratamiento no ha funcionado, la probabilidad de que haya sido tratado con el medicamento A es del 82%.
En la formula de arriba es interesante el denominador, ya que se trata de la probabilidad de que ocurra el efecto B, en este caso, un fracaso en el tratamiento, habra que sumar todas las probabilidades de fracaso para cada medicamento, es decir, la suma de los productos de la probabilidad de que se aplique un tratamiento con la probabilidad de que éste fracase, o lo que es lo mismo
P(A)P(F|A) + P(B)P(F|B) = P(F)
También es interesante notar que este teorema se centra precisamente en el hecho de que la probabilidad de que ocurra B habiendo ocurrido A no es la misma que la de que haya ocurrido A dado que haya ocurrido B. No es lo mismo la probabilidad de fracaso si se aplica el medicamento A, que la probabilidad de que hayamos aplicado el medicamento A si ha ocurrido un fracaso.
¡Espero que se haya entendido!
Referencias y créditos
He redactado este artículo en mi aprendizaje a partir de las siguientes fuentes:
- Curso Data Science: https://www.udemy.com/data-science-and-machine-learning-with-python-hands-on
- Bayes’ Theorem: https://www.youtube.com/watch?v=yWUTaQOwjxU