Cuando trabajamos con modelos de Inteligencia Artificial y Machine Learning, dejamos atrás la capacidad de saber con exactitud si los resultados que obtenemos son correctos o no, y nos adentramos en un mundo de grises donde hablamos más bien de probabilidades de acertar. En este post trato de resumir las principales técnicas con las que contamos para saber identificar si nuestro modelo de IA funciona suficientemente bien o si sería preferible lanzar una moneda al aire.
Índice de la serie de artículos
Iré actualizando esta sección a medida que vaya escribiendo más capítulos sobre el tema
- Introducción y clasificación
- Flujo de trabajo
- Validar el modelo
- Análisis exploratorio
- Algoritmos de Machine Learning:
- Supervisado:
Precisión de las predicciones
Por ejemplo, cuando usamos un modelo para predecir el valor de una casa en base a sus características de tamaño, ubicación, antiguedad, etc. es bastante obvio que no acertaremos hasta el último céntimo del precio por el que se venderá en el futuro, pero sí podremos calcular un valor estimado de lo cerca o lejos que estaremos de acertar, es decir, cuantos “euros” de margen de error tenemos en el resultado de nuestra predicción.
Si el valor predicho es suficientemente cercano al real, consideraremos que nuestro modelo es bueno, pero si está muy lejos, entonces será mejor hacer algo más de ingeniería hasta corregir esos resultados.
En este artículo resumiré cuales son algunas de las herramientas con las que contaremos para evaluar los resultados de nuestros modelos de aprendizaje, como necesitamos preparar los datos para realizar los cálculos, y otras utilidades para comparar modelos de predicción entre si.
Conjuntos de entrenamiento y test
A la hora de entrenar un modelo, lo más habitual será dividir el conjunto de datos en dos partes. Generalmente el 70-80% de los datos se destinará al entrenamiento, y el 30-20% restante se empleará para el testing.
Cuando hagamos el entrenamiento del modelo (model.fit) utilizaremos únicamente el conjunto de datos de entrenamiento, y nunca el de test.
El objetivo de esta separación es disponer de un conjunto de datos reales (e incluso supervisados) que nuestro modelo nunca ha visto durante el entrenamiento, por lo que no ha podido utilizar la información de sus características para ajustarse e él. Una vez que el modelo ha sido entrenado, podemos introducir los datos de test en el modelo entrenado y realizar predicciones (model.predict).
Los resultados de esta predicción se comparan con los reales que contenian las observaciones. Medimos así la diferencia entre el resultado del modelo y el dato real. Si la diferencia es pequeña, consideramos que el modelo es bueno, pero si está muy lejos o acierta pocas veces, tendremos que seguir trabajando para mejorarlo.
A la hora de seleccionar qué datos formarán parte de los conjuntos de entrenamiento y test, hay que tener cuidado de “por donde cortamos”. Si los datos estuviesen ordenados, por ejemplo, y cogiesemos para el entrenamiento el 80% del principio, el modelo no se entrenará conteniendo ninguno de los datos que estén al final. Una técnica básica pero eficaz consiste en seleccionar ese 80% aleatoriamente, de manera que los datos sean representativos. Tendremos que comprobar tambien que no haya sesgo, que los datos estén balanceados, etc. Y por supuesto los datos del conjunto del test deberían ser de una calidad similar.
En otras ocasiones, sin embargo, sí es recomendable mantener los datos ordenados, por ejemplo cuando estamos realizando predicciones sobre series temporales no tendría sentido desordenar la dimensión temporal porque perderíamos la correlación que existe en la secuencia de datos. Es cierto que las series temporales son un mundo a parte del que hablaré en otro post, pero es importante nunca dejar de entender lo que estamos haciendo cuando manipulamos los datos, o podríamos tener unos resultados aparentemente buenos pero que en realidad no significasen nada.
Overfitting
Esta separación también nos permite reconocer si se está produciendo un caso de overfitting. Hablamos de overfitting cuando el modelo entrenado se ha ajustado tanto a los datos de entrenamiento que no generaliza bien. Es decir, su precisión con los datos con los que ha sido entrenado es muy buena, pero los resultados con datos nuevos son muy malos.

Por ejemplo, en esta imagen de wikipedia, si usamos la linea verde como modelo entrenado, se ajustará perfectamente a los datos de entrenamiento, pero cuando aparecan datos nuevos, probablemente muchos se clasificarán mal. Si el modelo fuese más general (la linea negra) funcionaría de forma similar con ambos conjuntos de datos, el de entrenamiento y de test.
Otra forma de entender lo que sucede en un caso de overfitting, es considerar que el modelo recuerda los datos de entrenamiento muy bien, y por eso se ajusta a ellos, pero generaliza mal, por lo que los resultados para observaciones con las que nunca fue entrenado serian malos o al menos muy distintos a los del conjunto de entrenamiento.
Una forma de saber si tenemos un problema de overfitting, es viendo si la precisión de la predicción con el conjunto de entrenamiento, y con el conjunto de test es similar (no hay overfitting), o muy distinta (puede haberlo).
Conjunto de Validación
El conjunto de validación no es un conjunto separado de datos, sino más bien una técnica que se emplea para medir mejor el comportamiento de los modelos que implementemos y ajustar mejor sus parámetros.
La técnica de validación cruzada consiste en dividir el conjunto de entrenamiento en K subconjuntos, y realizar varias iteraciones para generar el modelo de aprendizaje. En cada una de las iteraciones, entrenaremos el modelo con K-1 de esos subconjuntos, es decir, usaremos todos los datos menos uno de los subconjuntos (uno distinto en cada iteración), que se empleará para medir la precisión del modelo obtenido en esa iteración.
Con esta técnica realizamos K=5 entrenamientos independientes, y calcularemos la precisión final de nuestro modelo haciendo la media de las 5 precisiones obtenidas en cada uno. Si el modelo funciona bien, las 5 precisiones serán similares entre si. Es una buena manera de asegurarnos de que no estamos siendo engañados porque casualmente el entreanmiento sobre un conjunto de datos especifico haya ido bien, o mal, ya que estamos realizando una media de varias mediciones. Eso si, el conjunto de datos debe ser suficientemente grande como para permitir cortarlo en conjuntos más pequeños sin perder mucha información en cada uno de ellos.
Si procuramos que los K subconjuntos tengas buen balanceo de clases, es decir, que como siempre el conjunto de datos sea equilibrado, esta técnica se conoce como Stratified K-Fold, y conseguiremos mejores resultados que con K-Fold (en la que no se controla esto).
Posteriormente, y como siempre, usaremos el conjunto de test que habiamos reservado para hacer una predicción y ver que sigue comportándose igual.
Medir la eficacia del modelo
Ya hemos visto como dividir y usar los datos para poder obtener métricas de eficacia realistas y lo más precisas posible. Ahora veamos cuáles son estas métricas y qué representa cada una. Los tipos de metricas varían en función de la técnica empleada.
Métricas empleadas en técnicas de regresión
Cuando el resultado de la predicción de un modelo es un valor numérico, estamos hablando de técnicas de regresión. Estas métricas se pueden obtener con las predicciones del conjunto de entrenamiento (Error de entrenamiento) o de test. En el primer caso siempre serán más pequeños los errores porque precisamente el modelo trata de minimizarlo, pero ambos nos ofrecerán información importante, como hemos visto antes, para detectar casos de overfitting o underfitting.
- Media de error o pérdida media: se mide la media del valor absoluto de la diferencia entre el resultado devuelto y del esperado (el real que debería haber devuelto). (Si fuese un modelo de clasificación podríamos considerar que el error es 1 si las categorias son distintas y 0 si ha acertado.)
- Error cuadrático medio o pérdida cuadrática: Si nuestro modelo hace predicciones que son anomalías, habra errores que sean muy grandes. Podemos detectarlo penalizando más los errores grandes, que es precisamente lo que hace esta métrica: calculando el cuadrado del la diferencia entre el resultado obtenido y el esperado.
- Raiz del error cuadrático medio: Realizando la raiz cuadrada del error cuadrático medio devolveremos la métrica a las mismas unidades originales para facilitar su comprensión.
- R^2, R-cuadrado, o coeficiente de determinación: Es un estadístico muy habitual que permite determinar la calidad del modelo para replicar los resultados y la proporcion de variación de los resultados que pueden explicarse con el modelo. En las regresiones lineales simples, se calcula como el cuadrado del coeficiente de correlación de Pearson. Se interpreta de manera que si por ejemplo obtenemos un 0,85, el modelo se ajusta bastante bien a la variable real, y diriamos algo así como que el modelo explica un 85% la variable real (aunque realmente no es exactamente así). Podemos comparar el coeficiente entre varios modelos y asumir que el que tenga el valor más alto será el que mejor explica la variable.
Métricas empleadas en técnicas de clasificación
Si el resultado del modelo de predicción es una clase, categoría o etiqueta, estamos hablando de técnicas de clasificación. Las métricas más habituales para comprender la eficacia del modelo son las siguientes:
- Matriz de confusión: Es una matriz donde en las columnas se pone el número de observaciones de cada categoria según ha predicho el modelo, enfrentado a la categoria real esperada, que ocupa el lugar de las filas.
-
Matriz de confusión en clasificación binaria: Es el mismo caso anterior pero cuando solo hay dos categorias posibles. En este caso es especialmente sencillo comprobar el comportamiento del modelo, y se suelen observar los siguientes valores:

- TN, True Negative o Verdadero negativo: El valor real era 0 y la predicción fue 0.
- FN, False Negative o Falso negativo: El valor real era 1 y la predicción fue 0.
- FP, False Positive o Falso positivo: El valor real era de 0 y la predicción fue de 1.
- TP, True Positive o Verdadero positivo: El valor real era de 1 y la predicción fue de 1.
- Precision = TP / (FP+TP): de todas las predicciones positivas, cuantas eran realmente positivas.
- Accuracy = (TN+TP) / (TN+TP+FN+FP): Porcentaje de predicciones correctas hechas por el modelo. Es muy adecuado unicamente cuando las clases están bien balanceadas, si no podría dar resultados confusos.
- Recall o Sensibilidad o TPR = TP / (TP+FN): Cuantos valores se han predicho como positivos de entre todos los que eran realmente positivos.
- Especificidad (Specificity) = TN / (TN+FP): Cuantos valores se han predicho como negativos de entre todos los que eran realmente negativos.
- FPR = 1 - Specificity: es la opuesta de la especificidad anterior y suele ser útil para representación y comprensión.
- Curva ROC: Gráfica que representa la sensibilidad frente a la especificidad de un sistema clasificador binario. Se representan los resultados de distintos modelos y se escoge el óptimo.
- AUC o área bajo la curva: a partir del gráfico anterior, mide la capacidad de un clasificador para distinguir entre las clases. Cuanto más alto el valor, mejor será capaz de distinguir entre clase positiva y negativa.
- Si AUC es 1, el modelo distingue perfectamente.
- Si AUC es 0, el modelo estaría prediciendo todos los valores 0 como 1, y todos los 1 como 0.
- Si AUC > 0.5, el clasificador permite distinguir los valores, porque detecta más Verdaderos positivos y negativos que Falsos positivos y negativos.
- SI AUC < 0.5, sería el caso contrario, y significa que no es capaz de distinguir entre positivos y negativos, la predicción es aleatoria.

Métricas en algoritmos de aprendizaje no supervisado
En este caso nuestro conjunto de datos no cuenta con una columna con el valor real que podamos contrastar con los predicciones obtenidas como resultado de nuestro modelo, por lo que las metricas anteriores no serán útiles, y se más dificil saber si el modelo implementado es adecuado o no.
En el caso de los algoritmos de clusterización de machine learning, analizaremos una serie de factores para validar que el modelo es óptimo. Por ejemplo, si los datos tienen una tendencia natural a la agrupación, es decir, que su distribución no sea realmente aleatoria y estén compactados en grupos, y que el número de clusters se ajusta al número real de grupos que hay en los datos. Además como siempre podremos enfrentar los resultados de los modelos observaciones reales, supervisadas o no supervisadas, para analizar su comportamiento y eficacia.
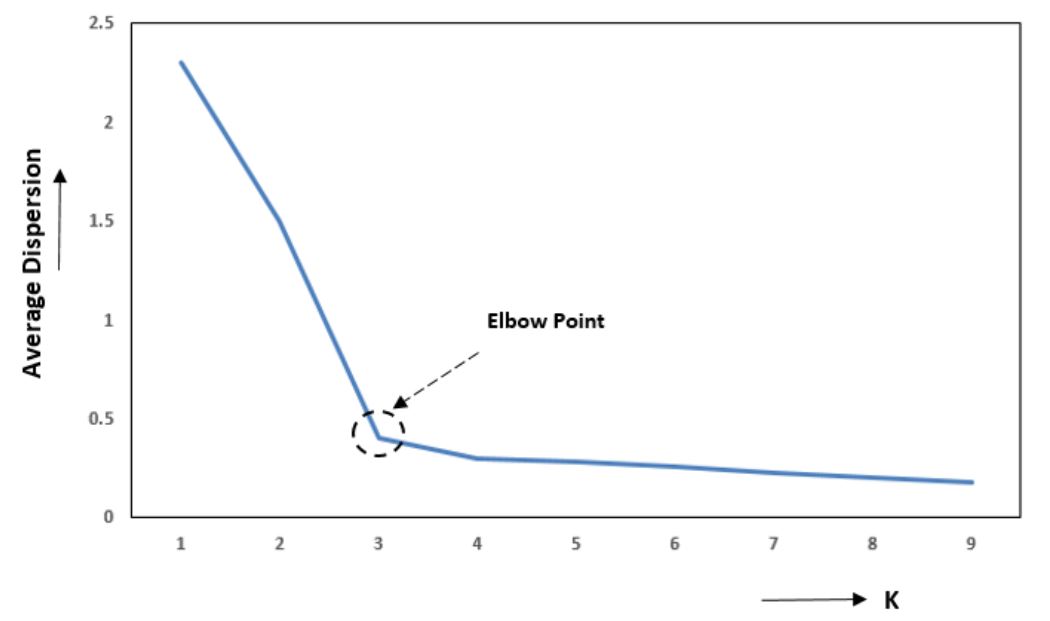
Método del codo
El método del codo permite comprobar que el número de clusters es adecuado al número de clusters. Para esto jugaremos con la distancia intracluster, es decir, la distancia de cada punto al baricentro del cluster y lo elevamos al cuadrado (suma de los cuadrados internos, o SSK), para ver si estos están o no realmente bien compactados (cuando más compacto, más claro y evidente será la presencia de un cluster).
Un mayor número de clusters, hará decrecer progresivamente el valor de SSK, siendo el caso extremo cuando tenemos tantos clusters como el número de elementos, ya que la distancia de todos los datos al centro de su cluster sería 0.
Se da la circunstancia de que si representamos en una gráfica este valor para cada valor posible de numero de clusters, se formará una curva que en algun punto cae rápidamente y luego desciende progresivamente con menor velocidad. En general, el valor óptimo será el núemero de clusters en el que la curva a dejado de decrecer rapidamente y comienza a estabilizarse.
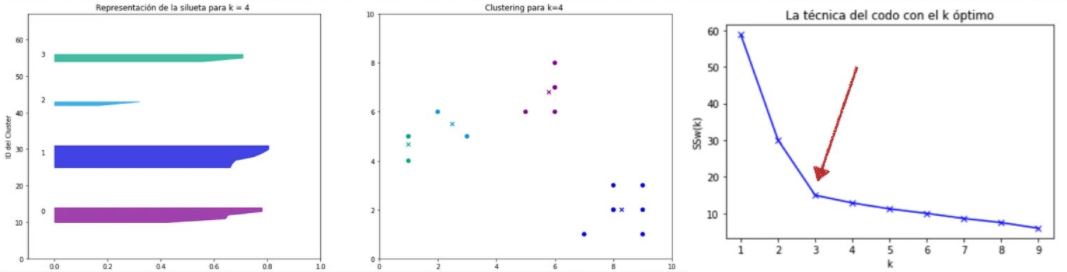
Método de coeficiente de la silueta
Nos ayuda a decidir tambien el número óptimo de clusters:
- El valor de a(i) identifica cómo de bien esta un punto unido al resto de puntos de su mismo cluster. Se calcula como el promedio de distancia del punto i a cada uno de los puntos del mismo cluster, por lo que será mejor cuanto más pequeño sea el valor.
- El valor de b(i) identifica cómo de bien está el punto separado cluster vecino más cercano, y se calcula como la distancia promedio del punto i a cualquier otro cluster que no contenga a i.
Se calcula el coeficiente de silueta, y su valor debería ser cercano a 1 para garantizar que está bien clasificado.
Se representa como en la imagen siguiente, donde cada cluster se representa con un color, y para cada punto se representa con una barra su coeficiente.
Si la silueta promedio de alguno de los clusters es muy inferior al promedio global, entonces el numero de clusters es suboptimo y necesitaremos recalcularlo con un número distinto de clusters, así hasta que las siluetas de todos los clusters sean similares.
Análisis exploratorio
En la siguiente parte, nos adentramos en lo esencial pare realizar el análisis exploratorio de los datos, lo que nos permite conocerlos y obtener las primeras intuiciones.
Nos vemos!