Después de unas cuantas dosis de teoría, vamos a empezar a adentrarnos en algunos ejemplos prácticos de aplicación de distintos algoritmos de ML comenzando por los Árboles de decisión, que me gustan mucho porque en sus versiones más sencillas, dejan muy claro al humano como funcionan.
Sé que quiza me estoy adelantando un poco metiendo código tan pronto, pero este artículo es muy introductorio y su propósito es únicamente permitir hacernos una idea de qué aspecto tiene una implementación básica de estas cosas de las que vengo escribiendo. Y además me apetecía un poquito de python.
Índice de la serie de artículos
Iré actualizando esta sección a medida que vaya escribiendo más capítulos sobre el tema
- Introducción y clasificación
- Flujo de trabajo
- Validar el modelo
- Análisis exploratorio
- Algoritmos de Machine Learning:
- Supervisado:
Árboles de decisión
Los árboles de decisión, árboles de regresión y random forest, son modelos diferentes entre si pero todos basados en diagramas lógicos que se construyen en base a secuencias de condiciones hasta alcanzar un extremo del árbol donde el problema de regresión o clasificación queda resuelto con un valor que es el estimado para esa hoja.
Se emplean en una gran cantidad de ámbitos y puede ser visualmente representado, por lo que a diferencia de otros modelos el resultado puede ser facilmente intrepretado y reproducido por un humano, simplemente siguiendo la serie de decisiones a medida que se avanza por el árbol.
Elementos del árbol
Los elementos fundamentales del árbol son los siguientes:
- Nodos: representa una decisión, que se bifurca en un número cada vez mayor de posibles resultados. Esta caracteristica es la que puede dificultar la lectura o la representacion en árboles muy complejos.
- Flechas: conectan nodos entre sí, y representan una acción o decisión.
- Hojas: se encuentran al final del arbol y son nodos que no conducen a ninguna otra decisión. Cada hoja tiene un resultado asociado, que seria el resultado de la decisión que se toma y para la que se emplea el árbol.
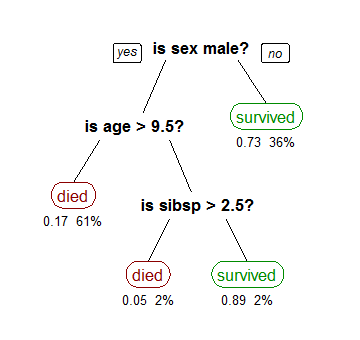
Sobreajuste y poda
Cuando trabajamos con árboles de decisión es frecuente oir hablar del concepto de poda. La poda consiste en eliminar ramas de nodos a partir de cierta profundidad en el árbol, convitiendo ese nuevo final en una hoja. Se obtiene un árbol menos complejo y sobre todo de menor profundidad.
Este técnica se emplea especialmente en casos de sobreajuste (overfitting) ya que los árboles de decisión o regresión (y en función de los parametros que empleemos en su creación), son muy sensibles a este tipo de problema, ya que las decisiones pueden propagarse hasta generar tantos nodos como sea posible, de manera que el arbol acaba teniendo incluso tantas hojas como observaciones hay en nuestro conjunto de entrenamiento.
Como ocurre en otros casos de overfitting, esto sería una mala generalización, y lo que tendríamos es un árbol que “recuerda muy bien el conjunto de entrenamiento, pero predice muy mal nuevas observaciones”.
Árbol de Regresión
En los árboles de regresión cada hoja tiene un valor estimado para la variable objetivo (como en otros casos de Regresión, lo que intentamos es predecir una variable numérica). Son modelos predictivos supervisados, donde cada nodo contiene preguntas y condiciones relacionadas con alguna de las covariables independientes presentes en el conjunto de entrenamiento.
Cada hoja contiene un valor de confianza en función del error posible para la variable en esa situación.
Ejemplo en Python
En primer lugar preparamos un datos de ejemplo. Los datos son característias del vehiculo (cilindrada, potencia, peso, aceleración…) y la variable de salida que deseamos calcular es mpg, un valor numérico que representa el consumo (miles per gallon of fuel).
## Arboles de regresión
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
## cargamos los datos
data = pd.read_csv("https://raw.githubusercontent.com/findemor/ml-with-python/main/jupyter-notebooks/datasets/vehiculos.csv")
data = data.dropna()
print(data.shape)
## Conjuntos de entrenamiento y prueba
from sklearn.model_selection import train_test_split
train, test = train_test_split(data, test_size = 0.2)
print("Entrenamiento: " + str(len(train)))
print("Test: " + str(len(test)))
## escogemos las columnas
columns = data.columns.values.tolist()
var_objetivo = columns[0]
var_independientes = columns[1:8]
X = train[var_independientes]
Y = train[var_objetivo]
## Resultado
# (392, 9)
# Entrenamiento: 313
# Test: 79
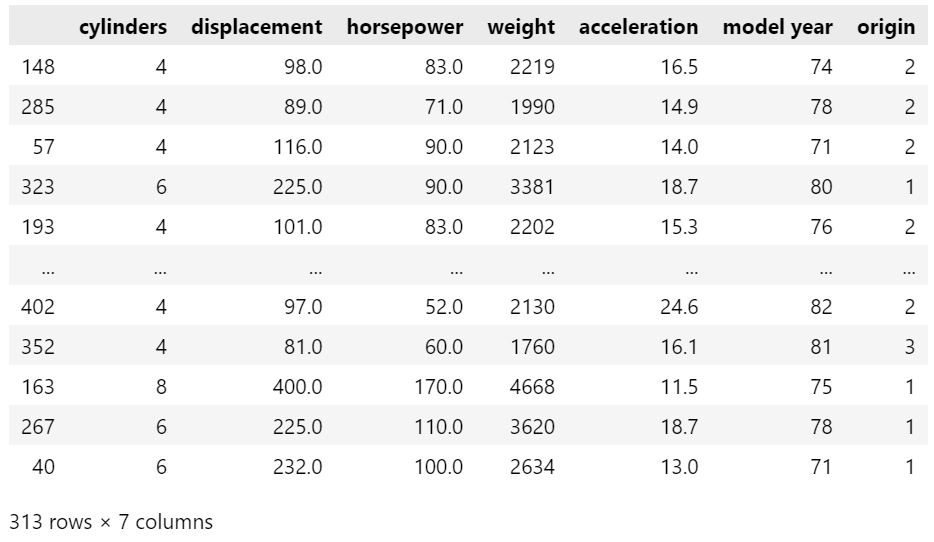
A continuación calculamos el arbol de regresión:
# Arbol de regresión
from sklearn.tree import DecisionTreeRegressor
# min_samples_split = observaciones minimas que debe haber para dividir el nodo en mas decisiones
# min_samples_leaf = si hay esta cantidad se considera que es una hoja
regression_tree = DecisionTreeRegressor(min_samples_split=20, min_samples_leaf=10, random_state=0)
regression_tree.fit(X,Y) ## entrenamiento del modelo
Ahora que el modelo está entrenado, podemos realizar algunas predicciones de ejemplo. Observamos que valores devuelve para algunas observaciones del conjunto de pruebas.
predicciones = regression_tree.predict(test[var_independientes])
df = test.copy()
df["predicciones"] = predicciones
df[["mpg","predicciones"]].head()
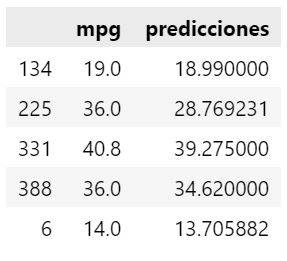
También es posible representar el árbol exportandolo a una imagen:
# Representación
from sklearn.tree import export_graphviz
import os
from graphviz import Source
with open("./regression_tree.dot", "w") as dotfile:
export_graphviz(regression_tree, out_file=dotfile, feature_names=var_independientes)
dotfile.close()
file = open("./regression_tree.dot", "r")
text = file.read()
Source(text)
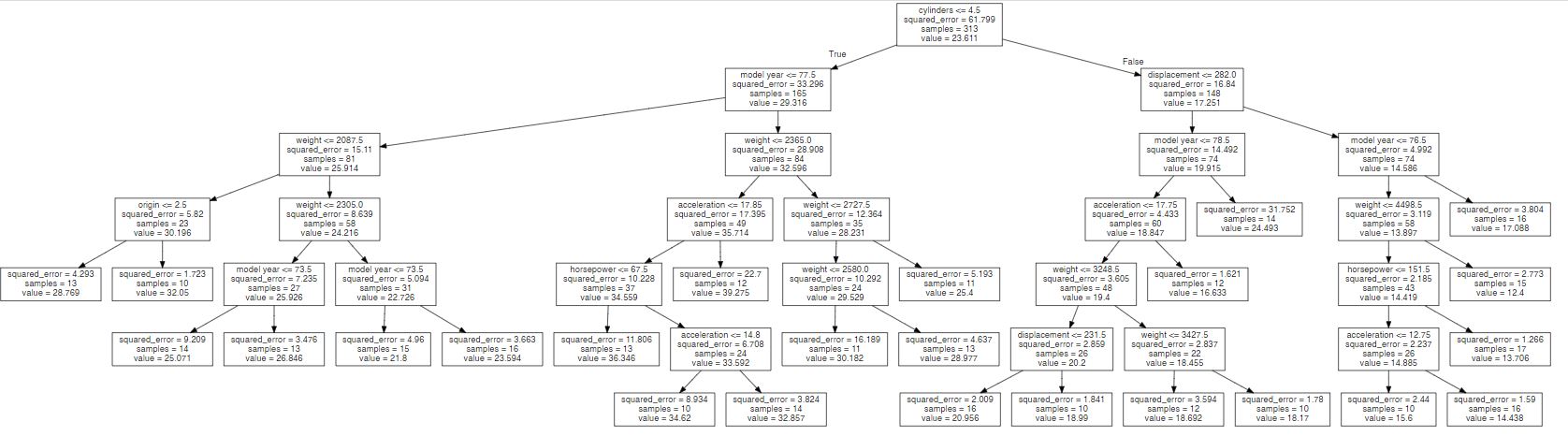
Finalmente podemos hacer una validación del modelo midiendo el error:
## Cross Validation
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
X = train[var_independientes]
Y = train[var_objetivo]
for i in range(4,10):
# modelo de aprendizaje
rtree = DecisionTreeRegressor(min_samples_split=i*2, min_samples_leaf=i, random_state=0)
rtree.fit(X,Y)
# hacemos las subdivisiones
conjuntos = KFold(n_splits= 10, shuffle=True, random_state=1)
eficacias = cross_val_score(rtree, X, Y, scoring="neg_mean_squared_error", cv = conjuntos, n_jobs = 1)
eficacia = np.mean(eficacias)
print('Eficacia para i [', i, " = ", eficacia, "]"", relevancias: ", rtree.feature_importances_)
### Resultados
# Eficacia para i [ 4 = -11.126745413415032 ], relevancias: [0.62372 0.064862 0.00448433 0.13607207 0.02734589 0.1365146 0.00700111]
# Eficacia para i [ 5 = -11.229777829483787 ], relevancias: [0.63426764 0.06107663 0.00729816 0.13709591 0.02203521 0.13352998 0.00469647]
# Eficacia para i [ 6 = -10.596254854297092 ], relevancias: [0.63896408 0.06223914 0.00701262 0.13422499 0.01874879 0.13407915 0.00473124]
# Eficacia para i [ 7 = -10.302643913344152 ], relevancias: [0.64348644 0.06264083 0.0071702 0.12853127 0.0190933 0.13431322 0.00476473]
# Eficacia para i [ 8 = -10.906652027415474 ], relevancias: [0.65107252 0.06158651 0.00552889 0.12193431 0.01923777 0.13581912 0.0048209 ]
# Eficacia para i [ 9 = -11.06553051842432 ], relevancias: [0.65356297 0.06182208 0.0036818 0.12113072 0.01719029 0.13777279 0.00483934]
Para 6 samples hemos obtenido un error de 10.59, es decir, estamos acertando “10.6 puntos arriba o abajo del valor real”.
Tambien podemos consultar cuales son las características de los datos han resultado más relevantes para el modelo (qué peso tiene cada una):
list(zip(var_independientes, regression_tree.feature_importances_))
[('cylinders', 0.6546022500522756),
('displacement', 0.0619203907811325),
('horsepower', 0.004510843112501045),
('weight', 0.12105941456427959),
('acceleration', 0.017373248003633185),
('model year', 0.13702728354437002),
('origin', 0.003506569941808123)]
Árbol de Decisión
Estos árboles son modelos de clasificación supervisados. Su estructura es igual que la de los árboles de regresión, con la diferencia de que cada hoja representa alguno de los valores posibles para la variable de salida, cuando ésta no toma valores numéricos sino categóricos.
Como ocurre en el árbol de regresión cada hoja contiene, además de la etiqueta resultante, un valor que representa la confianza en que ese resultado sea correcto, que es distinto en función de la distribución de posibles resultados para la variable en esa hoja en el conjunto de entrenamiento.
Ejemplo en Python
En este caso vamos a utilizar el clasico dataset de flores Iris, donde tenemos las características de distintas flores (longitud y anchura de los petalos y los sépalos) y una característica categórica de salida que es la especie a la que pertenece (setosa, virginica o versicolor).
En primer lugar cargamos y preparamos rápidamente los datos:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
iris = load_iris()
data = pd.DataFrame(iris['data'], columns = iris['feature_names'])
data['target'] = pd.Series(iris['target'], name = 'target_values')
data['target_name'] = data['target'].replace([0,1,2], [species for species in iris['target_names'].tolist()])
data.columns = ["Sepal.Length", "Sepal.Width", "Petal.Length", "Petal.Width", "SpeciesNumber", "Species"]
## conjuntos de entrenamiento y prueba
from sklearn.model_selection import train_test_split
train, test = train_test_split(data, test_size = 0.2)
print("Entrenamiento: " + str(len(train)))
print("Test: " + str(len(test)))
## Resultado
# Entrenamiento: 120
# Test: 30
data.head(3)
Construimos y entrenamos el modelo del árbol de decisión
from sklearn.tree import DecisionTreeClassifier
colnames = data.columns.values.tolist()
var_independientes = colnames[:4]
var_objetivo = colnames[5]
decision_tree = DecisionTreeClassifier(criterion="entropy", min_samples_split=20, random_state=99)
decision_tree.fit(train[var_independientes], train[var_objetivo]) # entrenamos el modelo
Ya podríamos realizar algunas predicciones a partir de las observaciones del conjunto de pruebas:
predicciones = decision_tree.predict(test[var_independientes])
O incluso ver como se comporta mediante una matriz de confusión:
# Examinamos la matriz de confusión
pd.crosstab(test[var_objetivo], predicciones, rownames=["Real"], colnames=["Prediccion"])
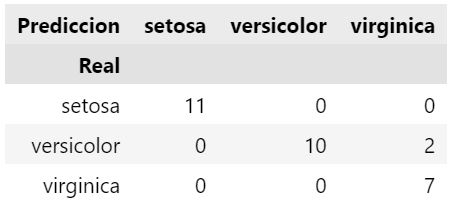
También ahora podríamos representar gráficamente el árbol de decisión generado:
from sklearn.tree import export_graphviz
import os
from graphviz import Source
### Generamos el fichero con la imagen de la representacion
with open("./decision_tree.dot", "w") as dotfile:
export_graphviz(decision_tree, out_file=dotfile, feature_names=var_independientes)
dotfile.close()
### leemos la imagen y la dibujamos
file = open("./decision_tree.dot", "r")
text = file.read()
Source(text)
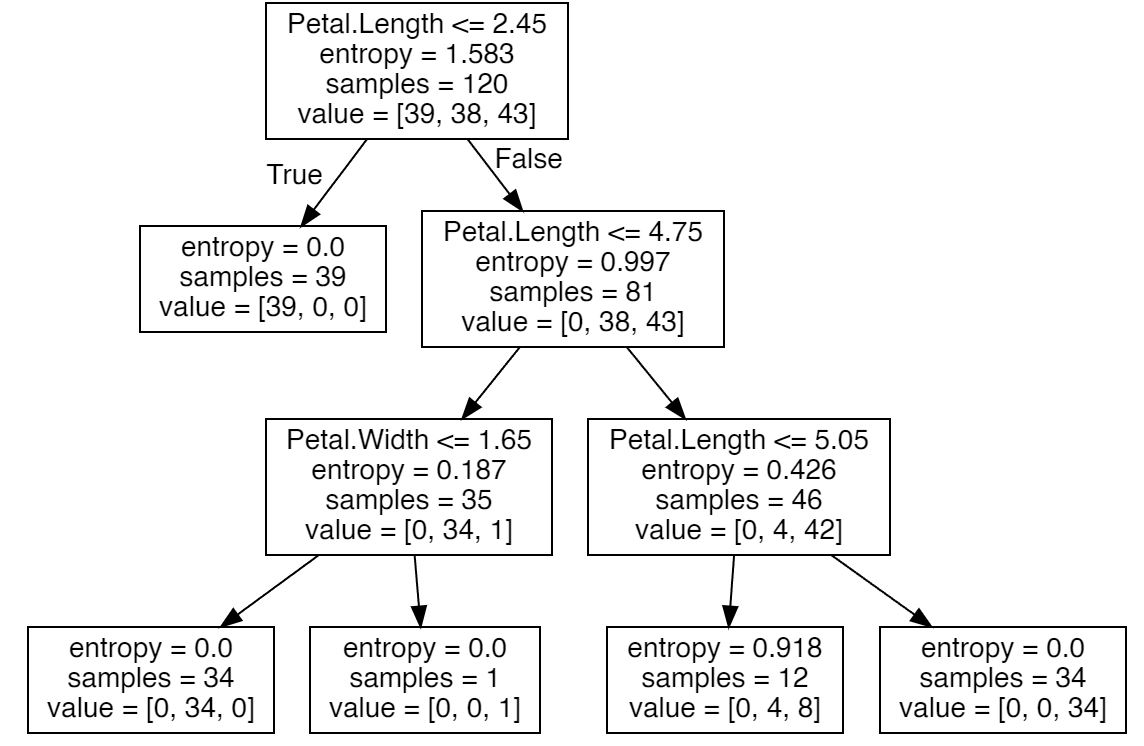
Y hacer cross validation para evaluar la eficacia del modelo:
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
X = train[var_independientes]
Y = train[var_objetivo]
for i in range(1,5):
# modelo de aprendizaje
dtree = DecisionTreeClassifier(criterion="entropy", max_depth=i, min_samples_split=20, random_state=80)
dtree.fit(X,Y)
# hacemos las subdivisiones
conjuntos = KFold(n_splits= 10, shuffle=True, random_state=1)
eficacias = cross_val_score(dtree, X, Y, scoring="accuracy", cv = conjuntos, n_jobs = 1)
eficacia = np.mean(eficacias)
print('Eficacia para i [', i, " = ", eficacia, "]"", relevancias: ", dtree.feature_importances_)
Eficacia para i [ 1 = 0.6333333333333334 ], relevancias: [0. 0. 0. 1.]
Eficacia para i [ 2 = 0.925 ], relevancias: [0. 0. 0.33347728 0.66652272]
Eficacia para i [ 3 = 0.9333333333333333 ], relevancias: [0. 0. 0.35325497 0.64674503]
Eficacia para i [ 4 = 0.9333333333333333 ], relevancias: [0. 0. 0.35325497 0.64674503]
Obtenemos un 93% de eficacia con profundidad 3.
Random Forest
Los Random Forest o Bosques aleatorios son una combinación de árboles de alguno de los tipos anteriores (regresión o clasificación). Un bosque aleatorio se construye dividiendo el conjunto de entrenamiento en un gran número de subconjuntos distintos y aleatorios. Cada uno de esos conjuntos se emplea para entrenar y generar un modelo de árbol de regresión o decisión distinto, obteniendo un gran número de modelos diferentes.
Cuando llega una nueva observación, se introduce en todos los árboles generados, y se obtienen tantos resultados como árboles hubiese en el bosque aleatorio. El resultado definitivo se obtiene promediando los valores obtenidos para cada uno de los árboles (en el caso de los árboles de regresión) o mediante votación del valor más frecuente (en el caso de los árboles de decisión).
Esta técnica es facil de entrenar y aplicar, y resuelve problemas habituales en los árboles de regresión y decisión, como el overfitting, o los producidos por desbalanceo en los conjuntos de entrenamiento, datos perdidos, datos ruidosos, etc. por lo que es una técnica muy habitual.
Ejemplo en Python
Vamos a ver rápidamente un ejemplo partiendo del arbol de decisión anterior.
from sklearn.ensemble import RandomForestClassifier
random_forest = RandomForestClassifier(n_jobs=2, oob_score=True, n_estimators=100)
random_forest.fit(X,Y)
# podemos ver lo que han consensuado los arboles (voto por mayoria) podemos ver cada observación en que categoría cae.
# random_forest.oob_decision_function_
# podemos consultar la evaluación del arbol (out of bag score)
# random_forest.oob_score_
Con el árbol de decisión entrenado podemos realizar predicciones como anteriormente:
random_forest.predict(test[var_independientes])
array(['virginica', 'virginica', 'versicolor', 'versicolor', 'setosa',
'setosa', 'virginica', 'setosa', 'virginica', 'virginica',
'virginica', 'virginica', 'setosa', 'virginica', 'virginica',
'versicolor', 'setosa', 'versicolor', 'setosa', 'versicolor',
'versicolor', 'virginica', 'versicolor', 'setosa', 'virginica',
'virginica', 'virginica', 'virginica', 'virginica', 'virginica'],
dtype=object)
Conclusión
Y hasta aquí esta introducción a este frecuente algoritmo de ML que són los árboles de decisión y regresión. Espero que os haya resultado interesante y os sirva para tener una idea general de qué aspecto tienen y cómo de complejo puede ser incorporarlos a vuestros sistemas de Machine Learning.
En el próximo post hablaremos de los modelos de regresión (lineal y polinomial) para abrir el camino a modelos de aprendizaje cada vez más interesantes.